Mehrfarbige Satinsäulen

Simulation einer mehrfarbigen Satinsäule

Wir sprechen hier von einer Simulation, da es sich nicht um eine einzelne mehrfarbige Satinsäule handelt, sondern um einen ähnlichen Effekt, der durch die Verwendung mehrerer übereinanderliegender Kopien derselben Satinsäule mit unterschiedlichen Parametereinstellungen erzielt wird.

Dieser Effekt kann nun ganz leicht mit Hilfe einer Ink/Stitch Erweiterung erzeugt werden.

Beginnen wir mit einer zweifarbigen Satinsäule

Kommen wir zurück zu den „zufälligen“ Parametern der Satinsäulen.

Zufälliger Prozentwert (Erweitern)

Der Parameter „Zufälliger Prozentwert (Erweitern)“ ist ein sogenannter asymmetrischer Parameter, da er auf beiden Seiten (Außenlinien) unterschiedlich angewendet werden kann. Dieser Parameter akzeptiert entweder einen einzelnen Wert, der auf jede der beiden Seiten angewendet wird, oder zwei durch Leerzeichen getrennte Werte, wobei in diesem Fall der erste auf die erste Seite und der zweite auf die zweite Seite angewendet wird.

• Wenn dieser Parameter auf 0 gesetzt ist, besteht die Säule (in Schwarz) aus Zickzacklinien, die zwischen den beiden Seiten verlaufen
• Wenn dieser Parameter auf 50 eingestellt ist, erstreckt sich jeder Zick (oder Zack) der Satinsäule (in Rot) nach links und rechts um einen Wert zwischen 0 und 50 % der Zickzacklänge. Die neue Satinsäule wird daher unregelmäßig verbreitert, höchstens kann sie doppelt so breit sein wie die schwarze (50 % links und 50 % rechts), aber nicht schmaler.
• Wenn dieser Parameter auf 0 50 gesetzt ist, bleibt die linke Seite der Satinsäule (in Grün) unverändert, aber auf der rechten Seite verlängert sie sich um bis zu 50 %.
• Wenn dieser Parameter auf 50 0 eingestellt ist, ist die Satinsäule (in Blau) ähnlich, nur links und rechts vertauscht.
• Wenn wir die drei Satinsäulen mit einem Wert ungleich Null für den Parameter überlagern, erscheint die Vergrößerung sehr zufällig, die Ränder der Satinsäule sind sehr unterschiedlich, auch wenn sie ähnlich sind.

Welche Werte kann dieser Parameter annehmen? Ink/Stitch akzeptiert hier jedes beliebige Zahlenwertpaar. Sie können positiv, null oder sogar negativ sein und den Wert 100 überschreiten. Auch wenn wir die Zickzacklinien unbegrenzt vergrößern können, ist die Reduzierung (durch negative Werte) de facto begrenzt, im schlimmsten Fall wäre der Zickzack ein einfacher Punkt auf der Mittellinie.

Zufälliger Prozentwert (Schrumpfen)

Satinsäulen haben auch den entgegengesetzten Parameter: „Zufälliger Prozentwert (Schrumpfen)“. Anstatt um -50 % zu erhöhen, können wir uns für eine Verringerung um 50 % entscheiden, das ist dasselbe.

Einfache, aber unvollkommene Methode

Dank eines dieser beiden Parameter verfügen wir bereits über eine erste unvollständige, aber sehr einfache Methode zur Simulation zweifarbiger Satinsäulen:

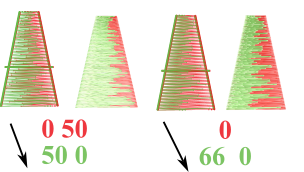
In beiden Beispielen wird „ufälliger Prozentwert (Schrumpfen)“ verwendet.

• Im linken Beispiel wird die linke Seite der roten Satinsäule reduziert, während die rechte Seite der grünen Satinsäule reduziert wird. Aber Vorsicht: die zweite Farbe überlagert die erste und hier verdeckt das Grün einen Teil des Rots.
• Auf der rechten Seite haben wir das Rot intakt gelassen, das Grün ist überlagert und auf der rechten Seite um bis zu zwei Drittel statt um die Hälfte reduziert.

Aber diese Methode ist unvollkommen: Sie stellt sicher, dass die gesamte Satinsäule gefärbt ist, es gibt keinen Mangel, aber es gibt eine gewisse Überlagerung.

Um zwei perfekt verbundene Satinsäulen zu erhalten ist jedoch die Verwendung zusätzlicher Zufallsparameter nötig.

Die Zufallszahl

Wenn wir mit einen oder mehrere Zufallsparameter verwenden und mit dem Ergebnis nicht zufrieden sind, können wir auf „würfeln“ klicken und ein anderes Ergebnis erhalten. Technisch gesehen bedeutet das erneute Würfeln, dass dem Parameter „Zufallszahl“ ein neuer Wert zugewiesen wird. Es ist auch möglich, diesem Parameter manuell einen Wert zuzuweisen. Dies ist besonders dann nützlich, wenn mehrere Kopien eines Objekts Zufallsparameter verwenden und tatsächlich vollkommen identisch sein sollen. Haben die Kopien die gleiche Zufallszahl, sind sie identisch.

Wenn wir das erste Beispiel wiederholen, aber diesmal allen drei Satinsäulen die selbe Zufallszahl geben, erhalten wir:

Wenn wir nun die drei Satinsäulen übereinander legen, sehen wir, dass die Ränder perfekt übereinander liegen. Die rote Satinsäule hat sich nach links genau wie die blaue Satinsäule und nach rechts genau wie die grüne Satinsäule erweitert. Trotzdem unterscheidet sich bei demselben Zick die Verbreiterung nach links von der Verbreiterung nach rechts.

Fast genauso einfache Methode, aber mit perfekter Passform (leider nicht allgemeingültig)

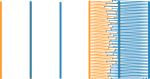
Dieses Mal werden zwei Satinsäulen nicht übereinander gelegt, sondern nebeneinander platziert. Der rechte Rand des einen wird über den linken Rand des anderen gelegt

• Beide Satinsäulen haben den gleichen Zufallsstartwert
• Die orangefarbene Satinsäule „Zufälliger Prozentwert (Schrumpfen)“ ist auf 50 0 eingestellt
• Die blaue Satinsäule „Zufälliger Prozentwert (Schrumpfen)“ ist auf -50 0 eingestellt (es handelt sich also um eine Zunahme).
• Zusätzlich haben wir für die blaue Satinsäule das Kästchen „Seiten umkehren“ aktiviert

Da beide die gleiche Zufallszahl haben und die Änderungen in beiden Fällen die erste Seite betreffen, liefert die Berechnung bei jedem Zickzack Werte, die eine perfekte Passung gewährleisten.

Leider lässt sich diese einfache Lösung nicht auf Satinsäulen beliebiger Form übertragen.

Für eine allgemeine Lösung verwenden wir noch einen weiteren zusätzlichen Parameter.

Zugkompensation (%)

Um mehrfarbige Satinsäulen zu erhalten, verwenden wir den Parameter „Zugkompensation (%)“.

Auch dieser Parameter ist asymmetrisch.

Es ist üblich diesem Parameter positive Werte zuzuweisen, es ist jedoch auch möglich, negative Werte festzulegen. Anstatt die Breite der Satinsäule zu vergrößern, verkleinern wir sie.

Hier ist das Ergebnis für drei verschiedene Werte für den Zugkompensation-(%)-Parameter:

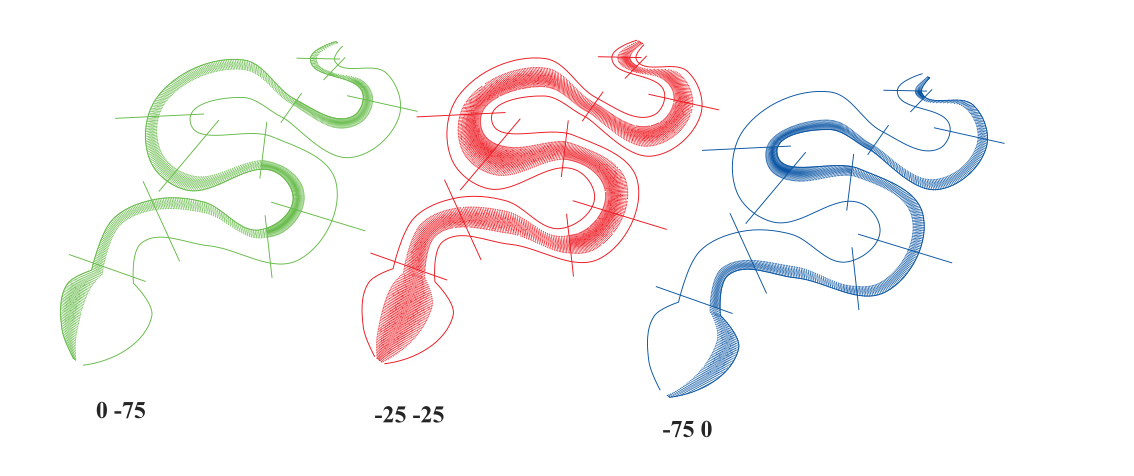
Hier ist die erste Seite die linke Seite der Satinsäule.

Wenn der Parameter auf „0 -75“ (grün) eingestellt ist, bleibt die linke Seite unverändert. Es sieht so aus, als ob die rechte Seite regelmäßig nach links verschoben worden wäre, um den Abstand zwischen den beiden Schienen auf ein Viertel des ursprünglichen Werts zu verringern. Wir sind tatsächlich von einer Breite von 100 % auf eine Breite von 100 - 75 = 25 % übergegangen.

Wenn der Parameter auf „-25 -25“ (rot) eingestellt ist, rücken die beiden Seiten näher zur Mitte und die Breite der Satinsäule wird gleichmäßig um die Hälfte reduziert.

Wenn der Parameter auf „-75 0“ (blau) eingestellt ist, berühren wir die rechte Seite nicht. Es sieht so aus, als ob die linke Seite nach rechts verschoben worden wäre, um den Abstand zwischen den beiden Schienen auf ein Viertel des ursprünglichen Wertes zu verringern.

Wenn wir diese drei Satinsäulen übereinander legen, erhalten wir eine dreifarbige Schlange.

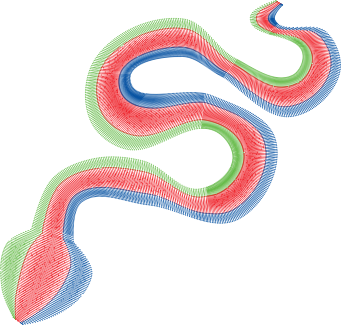
Info: Es ist möglich, die Zugkompensation in mm und die Kompensation in Prozent auf derselben Satinsäule zu verwenden. Beide Parameter sind asymmetrisch. Beide Paramxseter akzeptieren negative Werte.

Allgemeingültige Methode für zweifarbige Satinsäulen

Nun werden wir alle diese Parameter zusammen verwenden.

Wenn wir die 100 %-Breite der Satinsäule verteilen möchten

• L% links ausschließlich für Blau
• R% rechts ausschließlich für Grün
• und damit 100-(L+R) Prozent in der Mitte für eine Grün-Blau-Mischung,

werden wir folgende Einstellung verwenden:

Parameter	Blauer Satin	Grüner Satin
Zugkompensation (%)	0 100-L	0 100-R
Seiten umkehren	nein	ja
Zufälliger Prozentwert (Erweitern)	0 100-(L+R)	0
Zufälliger Prozentwert (Schrumpfen)	0	0 L+R-100
Zufallszahl	identisch	identisch

Wenn wir beispielsweise auf jeder Seite eine einzelne Farbe von 25 % beibehalten möchten, verwenden wir diese Einstellung

Blauer Satin:

• Zugkompensation (%): 0 -75
• Zufälliger Prozentwert (Erweitern): 0 50
• Zufälliger Prozentwert (Schrumpfen): 0
• Zufallszahl: 7 (oder eine beliebige Zahl oder ein beliebiges Wort (z.B. “Hallo”)

Grüner Satin:

• Zugkompensation (%): 0 -75
• Seiten umkehren
• Zufälliger Prozentwert (Erweitern): 0
• Zufälliger Prozentwert (Schrumpfen): 0 -50 (also eine Zunahme)
• Zufallszahl: 7 (oder was auch immer der Wert in der anderen Satinsäule ist)

Wichtig Wenn es nicht zu funktionieren scheint, lohnt es sich zu überprüfen, ob die Seiten der Satinsäulen beide in die gleiche Richtung zeigen und nicht automatisch korrigiert wurden. Überprüfe außerdem, ob kurze Stiche entfernt wurden.

Download die Schlangendatei

Jetzt könne wir mit mehr als nur zwei Farben spielen:

3 Farben

Angenommen, wir wollen 100 % der Breite von links nach rechts ausnutzen

• Das erste C1-Prozent ausschließlich in Farbe 1
• Die folgenden C1!2 Prozent werden zwischen Farbe 1 und Farbe 2 aufgeteilt
• Die folgenden C2-Prozentwerte ausschließlich in Farbe 2
• Die folgenden C2!3 Prozent teilen sich Farbe 2 und Farbe 3
• Der letzte C3-Prozentwert ausschließlich für Farbe 3

Für ein Ergebnis, das die Satinsäule ohne Überlauf perfekt füllt, muss C1+C1!2+C2+C2!3+C3 = 100 ergeben

Parameter	Farbe 1	Farbe 2	Farbe 3
Zugkompensation (%)	0 - (C1!2+C2+C2!3+C3)	-(C2!3+C3) -(C1+C1!2)	-(C1+C1!2+C2+C2!3) 0
Seiten umkehren	no	yes	no
Zufälliger Prozentwert (Erweitern)	0 C1!2	C2!3 0	0
Zufälliger Prozentwert (Schrumpfen)	0	0 - C1!2	-C2!3 0
Zufallszahl	identisch	identisch	identisch

Wenn wir also eine Unterteilung in Blau, Weiß und Rot ohne monochrome Zone wünschen, sind C1 = C2 = C3 = 0 und C1!2 = C2!3 = 50 und die Tabelle sieht wie folgt aus:

Parameter	Blau	Weiß	Rot
Zugkompensation (%)	0 -100	-50 -50	-100 0
Seiten umkehren	no	yes	no
Zufälliger Prozentwert (Erweitern)	0 50	50 0	0
Zufälliger Prozentwert (Schrumpfen)	0	0 -50	-50 0
Zufallszahl	identisch	identisch	identisch

Wenn wir lieber 20 % für jeden der monochromen Teile reservieren und den Rest gerecht aufteilen möchten, wählen wir C1 = C2 = C3 = 20, es bleiben 40 % übrig, also C1!2 = C2!3 = 20:

Parameter	Blau	Weiß	Rot
Zugkompensation (%)	0 -80	-40 -40	-80 0
Seiten umkehren	no	yes	no
Zufälliger Prozentwert (Erweitern)	0 20	20 0	0
Zufälliger Prozentwert (Schrumpfen)	0	0 -20	-20 0
Zufallszahl	identisch	identisch	identisch

4 Farben

Mit den gleichen Notationen haben wir jetzt

C1 + C1!2 + C2 + C2!3 + C3 + C3!4 + C4 = 100

Parameter	Farbe 1	Farbe 2	Farbe 3	Farbe 4
Zugkompensation (%)	0 C1-100	-(C2!3+C3+C3!4+C4) -(C1+C1!2)	-(C1+C1!2+C2+C2!3) -(C3!4 +C4)	0 C4-100
Seiten umkehren	nein	ja	nein	ja
Zufälliger Prozentwert (Erweitern)	0 C1!2	C2!3 0	0 C3!4	0
Zufälliger Prozentwert (Schrumpfen)	0	0 -C1!2	-C2!3 0	0 -C3!4
Zufallszahl	identisch	identisch	identisch	identisch

Alle Kompensationswerte sind negativ, alle Erhöhungen sind positiv, alle Verringerungen sind negativ.

Wenn wir dieses Mal keine monochrome Zone wünschen und eine gleichmäßige Aufteilung des Rests wünschen, gilt C1 = C2 = C3 = C4 = 0 und C1!2 = C2!3 = C3!4 = 33,3.

Wenn wir lieber 15 % für jeden der monochromen Teile reservieren und den Rest gerecht aufteilen möchten, wählen wir C1 = C2 = C3 = C4 = 15, es bleiben 40 % übrig, also C1!2 = C2!3 = C3!4 = 13.3.

Jede Farbanzahl

Um N Farben zu verwenden, wähle positive oder Nullwerte für die N monochromen Teile C1, C2, …. CN und die N-1 zweifarbigen Teile C1!2, C2!3, ….CN-1!N. Die Summe der 2N-1-Werte muss 100 betragen.

Erstelle eine Tabelle mit N Spalten

In der I-ten Spalte

I ist ungerade

Parameter	Farbe I
Zugkompensation (%)	C1+C1!C2+C2+C2!C3+…..C(I-1)!I CI!C(I+1)+C(I+1)+C(I+1)!(I+2)+…..CN
Seiten umkehren	no
Zufälliger Prozentwert (Erweitern)	0 CI!(I+1)
Zufälliger Prozentwert (Schrumpfen)	-C(I-1)!I 0
Zufallszahl	immer der gleiche Wert

Zugkompensation (%): Der erste Wert ist die Summe der Breiten für alles vor Farbe I und der zweite Wert ist die Summe der Breiten für alles nach Farbe I.

I ist gerade

Aktiviere Seiten umkehren, und invertiere die beiden Werte in den asymmetrischen Parametern.

Parameter	Farbe I
Zugkompensation (%)	CI!C(I+1)+C(I+1)+C(I+1)!(I+2)+…..CN C1+C1!C2+C2+C2!C3+…..C(I-1)!I
Seiten umkehren	yes
Zufälliger Prozentwert (Erweitern)	CI!(I+1) 0
Zufälliger Prozentwert (Schrumpfen)	0 -C(I-1)!I
Zufallszahl	immer der gleiche Wert

• Für die erste Spalte ist C(-1) = 0, wenn wir kein Überlaufen wünschen. Wir können hier einen positiven Wert setzen, wenn wir wollen, dass die erste Farbe nach links überläuft.
• Ebenso wird für die letzte Spalte C(N+1) = 0 angenommen, wenn wir nicht möchten, dass die letzte Farbe aus der Form heraustritt.

Und hier hast du einen Regenbogen …

In diesem Beispiel laufen die erste und letzte Farbe über

Download the rainbow file

Hinweis Für eine gute Stickqualität muss auch ein Zugausgleich hinzugefügt werden, um … den Zug auszugleichen! Werden die Farben so gestickt wie beschrieben, können Lücken zwischen den einzelnen Farben entstehen, da die Stiche die Stickerei verzerren. Am einfachsten ist es, etwas Zugkompensation (mm) hinzuzufügen. Es wird empfohlen eine weitere Kopie der Satinsäule ohne negative Zugkompensation, ohne Zufallsparameter, aber mit einer maximalen Stichlänge von 4 mm und einem breiten Zickzackabstand als Unterlage hinzuzufügen. Wähle eine Farbe, die der Farbe des Stoffes ähnelt.