Multicolor Satin
Multi-colored satin column Simulation
We are talking simulation here, because it is not a single multicolored satin column, but a similar effect obtained by using several superimposed copies of the same satin column, simply using different parameters settings.
This is now an Ink/Stitch extension
Let’s start with a bicolor satin
Let’s come back to the “random” parameters of the satin columns.
Random percentage of satin width increase
The “Random percentage of satin width increase” parameter is a so-called asymmetric parameter because it is possible to apply it differently on the two rails. This parameter accepts either a single value, applied to each of the two rails or two space separeted values, in which case the first is applied to the first rail, the second to the second rail.

- When this parameter is set to 0, the column (in black) is made up of zig-zags traveling between the two rails
- When this parameter is set to 50, each zig (or zag) of the column (in red) extends to the left and right by a value between 0 and 50% of the length of the zig. The new column is therefore irregularly widened , at most it can be twice as wide as the black one (50% on the left and 50% on the right), it is never narrower.
- When this parameter is set to 0 50, the left side of the column (in green) is unchanged, but on the right it extends up to a 50% additional length.
- When this parameter is set to 50 0, the column (in blue) is similar , just swapping left and right.
- If we superimpose the three columns having a non-zero value for the parameter, the enlargement seems very random, the borders of the columns are very different, even if they are similar.
What values can be entered in this parameter? Ink/Stitch accepts any pair of numeric values here. They can be positive, null or negative and they can exceed the value 100. However, if we can increase the zigs without limit, the reduction is de facto limited, at worst the zig would be a simple point on the center line.

Random percentage of satin width decrease
Satin columns also have the opposite parameter, the “Random percentage of satin width decrease “. Rather than increasing by -50%, we can decide to decrease by 50%, it’s the same thing.
Simple, but imperfect method
Thanks to any of these two parameters, we already have a first imperfect but very simple method for simulating bicolor satin columns:
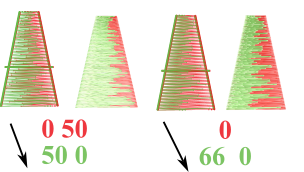
Both examples use “random percentage of width decrease”
- On the left example the left side of the red column is reduced while the right side of the green column is reduced. But be careful, the second color superimposes the first and here the green hides part of the red.
- On the right, we left the red intact, the green is superimposed, its right side reduced by up to two thirds rather than one half.
But this method is imperfect: it ensures that the entire column is colored, there is no lack, but there is some overlay.
It is possible to obtain two perfectly joining columns, but requires using additional random parameters
The random seed
Each time we use one or more random parameters, if we are not happy with the result, we can click on “reroll the dice” and obtain a different result. Technically, rerolling the dice means giving a new value to the “random seed” parameter. It is also possible to manually give a value to this parameter. This is particularly useful when one want several copies of an object that uses random parameters to be in fact perfectly identical. Give them the same random seed value and they will be identical.
If we repeat the first example but this time give all three columns the same random seed value, we get:

Now when we superimpose the three columns, we see that there is a perfect superposition of the borders. The red column has expanded to the left exactly like the blue column and to the right exactly like the green column. On the other hand, for the same zig, the widening to the left is different from the widening to the right.
Method almost as simple, with perfect fit but unfortunately not general
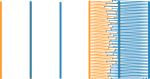
This time, instead of superimposing two columns, they are placed next to each other. The right edge of one being superimposed on the left edge of the other
- Both columns have the same random seed
- The orange column “Random percentage of satin width decrease “ is set to 50 0
- The blue column “Random percentage of satin width decrease “ is set -50 0 (so it is an increase).
- In addition, we have checked the Swap rails box for the blue column
As both have the same random seed and the modifications in both cases concern the first rail, at each zig the calculation gives values which ensure a perfect fit.
Unfortunately, this simple solution does not generalize to columns of any shape.
For a general solution, we’ll use yet another additional parameter:
Pull compensation percentage
To obtain multi-colored satin columns, we will use the “pull compensation percentage” parameter.
It is also an asymmetric parameter.
It is common to give positive values to the compensations, but it is also possible to give them negative values, instead of increasing the width of the satin column, we reduce it.
Here is the result for three different values for the pull compensation percentage parameter:
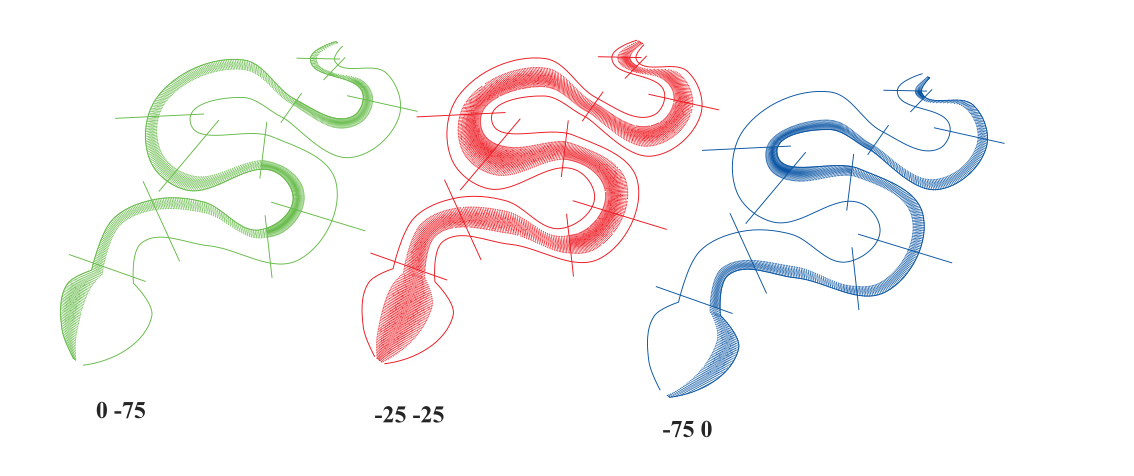
Here the first rail is the left side of the satin.
When the parameter is set to “0 -75” (in green) the left side is unchanged, but everything looks as if the right side had been moved to the left regularly to reduce the distance between the two rails to a quarter of the initial value. We have in fact gone from a width of 100% to a width of 100-75=25%
When the parameter is set to “-25 -25” (in red) the two edges move closer to the center and the width of the column is uniformly reduced by half.
When the parameter is set to “-75 0” (in blue) we do not touch the right side, but everything looks as if the left side had been moved to the right to reduce the distance between the two rails to a quarter of the initial value.
If we superimpose these three columns, we obtain a tricolor snake.
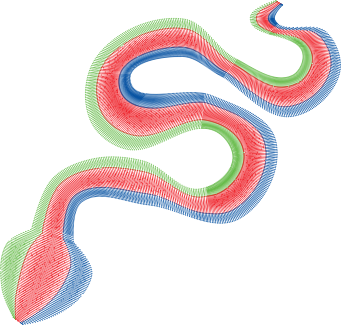
Notice: It is possible to use pull compensation in mm and compensation in percentage on the same satin column. Both parameters are asymmetrical. Both parameters accept negative values.
General method for bicolor satin column
We will use all these parameters together.
If we want to distribute the 100% width of the column into
- L% on the left exclusively for blue
- R% on the right exclusively for green
- and therefore 100-(L+R) percent in the middle for a green-blue mix,
we will use this setting
| Parameter | Blue satin | Green satin |
|---|---|---|
| Pull Compensation Percentage | 0 100-L | 0 100-R |
| Swap Rails | no | yes |
| Random satin width increase | 0 100-(L+R) | 0 |
| Random satin width drecrease | 0 | 0 L+R-100 |
| Random Seed | identical | identical |
So for example if we want to keep a 25% single color on each side, we will use this setting
Blue satin:
- Pull compensation percentage: 0 -75
- Random satin width increase: 0 50
- Random satin width decrease: 0
- Random seed: 7 (or “hello” or anything else but enter a value)
Green satin:
- Pull compensation percentage: 0 -75
- Check Swap Rails
- Random satin width increase: 0
- Random satin width decrease: 0 -50 (so it will be an increase)
- Random seed: 7 (or whatever you entered for the other column)
Important If it doesn’t seem to be working, check that the satin column rails are both in the same direction, and not automatically corrected. Also check that the short stitches are not triggered.

Download the snake file
We can play with many more than just two colors:
For three colors
Assuming that we want to distribute 100% of the width from left to right in
- The first C1 percent in color 1 exclusively
- The following C1!2 percent shared between Color 1 and Color 2
- The following C2 percent in color 2 exclusively
- The following C2!3 percent shared between Color 2 and Color 3
- The last C3 percent exclusively for Color 3
For a result that perfectly fills the column without any overflow, you must ensure that C1+C1!2+C2+C2!3+C3 = 100
| Parameter | Color 1 | Color 2 | Color 3 |
|---|---|---|---|
| Pull Compensation Percentage | 0 -(C1!2+C2+C2!3+C3) | -(C2!3+C3) -(C1+C1!2) | -(C1+C1!2+C2+C2!3) 0 |
| Swap Rails | no | yes | no |
| Random satin width increase | 0 C1!2 | C2!3 0 | 0 |
| Random satin width decrease | 0 | 0 -C1!2 | -C2!3 0 |
| Random Seed | identical | identical | identical |
So if we want a division into blue, white, red with no monochrome zone, C1,C2 and C3 will be equal to 0 and C1!2=C2!3=50 and the table becomes:
| Parameter | Blue | White | Red |
|---|---|---|---|
| Pull Compensation Percentage | 0 -100 | -50 -50 | -100 0 |
| Swap Rails | no | yes | no |
| Random satin width increase | 0 50 | 50 0 | 0 |
| Random satin width decrease | 0 | 0 -50 | -50 0 |
| Random Seed | identical | identical | identical |
if we rather wish to reserve 20% for each of the monochrome parts and share the rest equitably, we choose C1=C2=C3=20, there is 40% remaining so C1!2=C2!3=20 and the table becomes:
| Parameter | Blue | White | Red |
|---|---|---|---|
| Pull Compensation Percentage | 0 -80 | -40 -40 | -80 0 |
| Swap Rails | no | yes | no |
| Random satin width increase | 0 20 | 20 0 | 0 |
| Random satin width decrease | 0 | 0 -20 | -20 0 |
| Random Seed | identical | identical | identical |

For four colors
With the same notations we will have this time
C1+C1!2+C2+C2!3+C3+C3!4+C4 =100
| Parameter | Color 1 | Color 2 | Color 3 | Color 4 |
|---|---|---|---|---|
| Pull Compensation Percentage | 0 C1-100 |
-(C2!3+C3+C3!4+C4) -(C1+C1!2) |
-(C1+C1!2+C2+C2!3) -(C3!4 +C4) |
0 C4-100 |
| Swap Rails | no | yes | no | yes |
| Random satin width increase | 0 C1!2 | C2!3 0 | 0 C3!4 | 0 |
| Random satin width drecrease | 0 | 0 -C1!2 | -C2!3 0 | 0 -C3!4 |
| Random Seed | identical | identical | identical | identical |
All compensation values are negative, all increases are positive, all decreases are negative.
This time, if we do not want a monochromous zone and wish an equal sharing of the rest, C1=C2=C3=C4=0 and C1!2=C2!3=C3!4=33.3.
If we rather wish to reserve 15% for each of the monochrome parts and share the rest equitably, we choose C1=C2=C3=C4=15, there is 40% remaining so C1!2=C2!3=C3!4=13.3

For any number of colors
To use N colors, choose positive or zero values for the N monochrome parts C1,C2,…..CN and the N-1 two-color parts C1!2, C2!3, ….CN-1!N. The sum of the 2N-1 values must be 100.
Prepare a table with N columns
In the i-th column
If i is odd
| Parameter | Color I |
|---|---|
| Pull Compensation Percentage | C1+C1!C2+C2+C2!C3+…..C(I-1)!I CI!C(I+1)+C(I+1)+C(I+1)!(I+ 2)+…..CN |
| Swap Rails | no |
| Random satin width increase | 0 CI!(I+1) |
| Random satin width decrease | -C(I-1)!I 0 |
| Random Seed | always_the_same_thing |
The pull compensation percentage first value is the sum of the widths for everything before color I, and the second value is the sum of the widths for everything after color I.
If i is even
Check Swap rails, and invert the two values in each asymetrical parameter.
| Parameter | Color I |
|---|---|
| Pull Compensation Percentage | CI!C(I+1)+C(I+1)+C(I+1)!(I+2)+…..CN C1+C1!C2+C2+C2!C3+…. .C(I-1)!I |
| Swap Rails | yes |
| Random satin width increase | CI!(I+1) 0 |
| Random satin width decrease | 0 -C(I-1)!I |
| Random Seed | always_the_same_thing |
- For the first column C(-1) is equal to 0 if we do not want overflow, we can give it a positive value, if we want the first color to overflow to the left.
- Likewise for the last column C(N+1) will be taken equal to 0 if we do not want the last color to overflow the shape.
And here you havea r ainbow…..
For this example, the first and last color overflow
Download the rainbow file
Note For a good quality embroidery, you must also add some pull compensation to… compensate for… the pull! Embroidered as is the colors will not look quite joined together, as the stitches distort the embroidery. The easiest way is to add a little bit of pull compensation in mm. It is also a good idea to add yet another copy of the column with no negative pull compensation , no random parameters, but a 4mm maximum stitch length and a wide zigzag spacing to act as an underlay. Chose a color close to your fabric’s color.
